“Eurika! (I have found)”… Shouted Archimedes after he sunk in his bathtub, but did you know that the discovery behind that Eurika is the reason why ships float?
The principle of buoyancy
Imagine being Archimedes, casually taking a bath and finding out as you sink in that “The upward buoyant force that is exerted on a body immersed in a fluid, whether partially or fully submerged, is equal to the weight of the fluid that the body displaces and acts in the upward direction at the center of mass of the displaced fluid”.
Simply put, gravity exerts a downward force on the boat, attempting to pull it down into the water. To remain afloat, the boat must create an upward force that is equal to or greater than its weight.
The Formula for Archimedes’ Principle can be given as:
Fb = ρ x g x V
- Fb = buoyant force
- g = acceleration due to gravity
- ρ = density
- V = volume
Volume
According to Archimedes’ principle, an object will float as long as the volume of water it displaces is equal to or greater than the weight of the object.
This is also based on Newton’s first law. In the first law, an object will not change its motion unless a force acts on it. If the force of buoyancy pushing upwards is equal to the force of the weight pushing downwards, then the sum of these forces is zero, not changing the motion of the object.
For example, if a vessel weighs 100,000 tons, it will float as long as the volume of water it displaces is equal to 100,000 tons.
Density
Density is a measure of how much mass is contained in a given volume. It is typically expressed as mass per unit volume.
When an object is immersed in water, it either floats or sinks based on the density of the object and the liquid. However, there is a paradox here: a block of steel thrown in the sea will sink straight to the bottom because it is denser than water but ships that weigh million tons float effortlessly. The reason? Empty space.
Air is a lot less dense than water, so all that empty space packed along with people and cargo makes the construction float. That is the reason why when there is a breach onboard and water enters the vessel, replacing the air, the boat will most likely sink.
Why do ships stay afloat?
We may have explained the reason why ships float, but how does a vessel withstand treacherous seas and high winds without tipping over? The answer lies in weight distribution and stability.
The optimal weight distribution is determined by considering the weight and buoyancy of the entire boat, ensuring that it remains balanced and afloat. The correct calculation and adjustment of these factors are vital for the seaworthiness and stability of the boat.
Center of buoyancy (CB)
The center of buoyancy is the centroid of the displaced water volume. When a ship is upright, this point is located directly below the center of gravity (G) of the ship. As explained, buoyancy exercises an upwards force on the vessel, equal to the vessel’s weight.
Center of Gravity (CG)
The center of gravity is the point through which the entire weight of the ship acts vertically downward. Stability increases when the center of gravity is kept low. The distribution of weight, including cargo, fuel, and other components, is carefully managed to maintain a low center of gravity.
The interaction between these two points contributes to stability. If the ship tilts due to external forces (like waves or wind), the righting arm creates a turning moment that tries to return the ship to an upright position.
When the ship starts to tilt, the force of buoyancy generates a turning moment that tends to return the ship to an upright position. However, if the CG is high, the force of buoyancy, instead of stabilizing the ship, exacerbates the tilt. This is because the moment created by the force of buoyancy at the lower CB is trying to rotate the ship in the opposite direction to the tilt, while the high CG resists this rotational force.
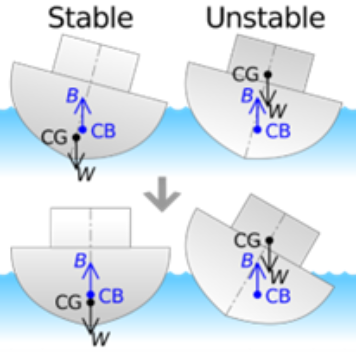
In simple terms, when the ship tilts, the force of buoyancy doesn’t effectively counteract the tilt, and instead, it contributes to the ship leaning even more, exceeding the stability limits of the vessel. This can be a precarious situation and can potentially lead to capsizing if not corrected.
Engineers and naval architects carefully design ships to ensure a low and well-balanced center of gravity to maintain stability in various conditions.
Distribution of mass
Engineers also ensure that the mass of the ship is evenly distributed, especially below the waterline. This balanced distribution helps prevent excessive tilting or leaning in response to waves or wind.
Stabilization Systems
Some modern ships employ active stabilization systems, such as fins, to counteract the rolling motion caused by waves. These systems help maintain a smoother ride and reduce the risk of tipping.
Furthermore, ballast tanks allow for the adjustment of the ship’s weight distribution. By taking on or releasing ballast water, the vessel can adapt to different sea conditions, optimizing stability.








































































































































